Mikroøkonomi - 3.1 Marginalprodukter og MRTS
Denne opskrift lærer dig, hvordan du finder marginalproduktet for de to inputs i en produktionsfunktion.
Sørg for at du kender regnereglerne for differentiering.
Hvis du har styr på marginalnytter og MRS fra forbrugerteori, så er det her fuldstændig det samme bare med lidt andre navne.
At finde marginalprodukt og MRTS vil ofte være det første skridt i en opgave, hvor du skal udregne hvilken blanding af inputs, der minimerer omkostninger ved et givet output (eller hvordan man maksimerer output ved givne omkostninger).
Derfor skal vi kunne udregne dette, før vi går videre, med andre opskrifter inden for produktionsteori
Gennemgang inkl. regneeksempel
Tims Chokoladefabrik producerer chokoladefrøer (Q) ved hjælp af arbejdskraft (L) og maskiner (K).
Eksempel 1:
Produktionsfunktionen er givet ved:
Trin 1: Find marginalproduktet for input L ved at differentiere produktionsfunktionen med hensyn til L som den variable, mens K behandles som en konstant
Vi differentierer produktionsfunktionen med hensyn til L. Bemærk at vi behandler K som en konstant, dvs. at de regneregler der gælder for konstanter gælder for K: Hvis den er ganget på den variable, bliver den stående, hvis den er plusset eller minusset på bliver den til 0. I dette tilfælde er K ganget på L og derfor lader vi den stå. Vi lader den være som den er og skal heller ikke gøre noget ved potensen:
Trin 2: Find marginalproduktet for input K ved at differentiere produktionsfunktionen med hensyn til K som den variable, mens L behandles som en konstant
Vi differentierer nu produktionsfunktionen med hensyn til K. Der er altså nu L, som skal behandles som en konstant:
Løsningen kort fortalt
Trin 1:
Find marginalproduktet for input L ved at differentiere produktionsfunktionen med hensyn til L som den variable, mens K behandles som en konstant
Trin 2:
Find marginalproduktet for input K ved at differentiere produktionsfunktionen med hensyn til K som den variable, mens L behandles som en konstant
Trin 3:
Find MRTS ved at dividere marginalproduktet for L med marginalproduktet for K. Hvis produktionsfunktionen er en Cobb-Douglas funktion, kan du bruge en bestemt formel
Trin 4:
Reducer udtrykket for MRTS så meget som muligt
Trin 3: Find MRTS ved at dividere marginalproduktet for L med marginalproduktet for K. Hvis produktionsfunktionen er en Cobb-Douglas funktion, kan du bruge en bestemt formel
Produktionsfunktionen er i dette tilfælde en Cobb-Douglas funktion. Vi kan genkende en Cobb-Douglas funktion når den har følgende struktur:
hvor A, α og β er konstanter
Vores produktionsfunktion matcher denne form:
Når produktionsfunktionen er en Cobb-Douglas funktion kan man anvende følgende formel for MRTS:
Vi anvender denne formel og udregner MRTS:
For træningens skyld, beregner vi også MRTS ved hjælp af den normale formel:
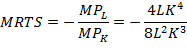
Reduceres dette udtryk skulle det gerne blive det samme som ovenstående.
Trin 4: Reducer udtrykket for MRTS så meget som muligt
Når vi skal reducere brøken, skal vi bruge to potensregneregler. Den første siger, at hvis den samme variabel står i tælleren og i nævneren kan vi trække den nederste potens fra den øverste:
Den anden siger, at man i stedet for at gange med en variabel kan dividere med den (eller omvendt), på den betingelse at potensen skifter fortegn:
Vi anvender disse regler og reducerer MRTS så meget som muligt:
Bemærk at vi også reducerer konstanterne 4 over 8 til 1 over 2 ved at dividere begge tal med 4.
Eksempel 2:
Produktionsfunktionen er givet ved:
Trin 1: Find marginalproduktet for input L ved at differentiere produktionsfunktionen med hensyn til L som den variable, mens K behandles som en konstant
Vi differentierer produktionsfunktionen med hensyn til L. Bemærk at vi behandler K som en konstant, dvs. at de regneregler der gælder for konstanter gælder for K: Hvis den er ganget på den variable, bliver den stående, hvis den er plusset eller minusset på bliver den til 0. I dette tilfælde er K plusset på L og derfor bliver den til 0, dvs. den forsvinder. L er den variable og har kun 1 i potens, derfor bliver den til et 1-tal. Da K-leddet forsvinder og L bliver til 1, har vi egentlig kun 2 tilbage:
Trin 2: Find marginalproduktet for input K ved at differentiere produktionsfunktionen med hensyn til K som den variable, mens L behandles som en konstant
Vi differentierer nu produktionsfunktionen med hensyn til K. Der er altså nu L, som skal behandles som en konstant:
Trin 3: Find MRTS ved at dividere marginalproduktet for L med marginalproduktet for K. Hvis produktionsfunktionen er en Cobb-Douglas funktion, kan du bruge en bestemt formel
Produktionsfunktionen er i dette tilfælde ikke en Cobb-Douglas funktion. Vi kan derimod se at de to inputs er perfekte substitutter da L og K er plusset på hinanden og begge blot har 1 i potens. Herved får vi rette linjer som indifferenskurver, og MRTS skal derfor blive en konstant (husk at MRTS er hældningen på isokvanten):

Trin 4: Reducer udtrykket for MRTS så meget som muligt.
Her kan MRTS ikke reduceres yderligere.
Eksempel 3:
Produktionsfunktionen er givet ved:
Trin 1: Find marginalproduktet for input L ved at differentiere produktionsfunktionen med hensyn til L som den variable, mens K behandles som en konstant
Vi differentierer produktionsfunktionen med hensyn til L. Bemærk at vi behandler K som en konstant, dvs. at de regneregler der gælder for konstanter gælder for K: Hvis den er ganget på den variable, bliver den stående, hvis den er plusset eller minusset på bliver den til 0. I dette tilfælde er K plusset på L og derfor bliver den til 0, dvs. den forsvinder:
Trin 2: Find marginalproduktet for input K ved at differentiere produktionsfunktionen med hensyn til K som den variable, mens L behandles som en konstant
Vi differentierer nu produktionsfunktionen med hensyn til K. Der er altså nu L, som skal behandles som en konstant. Da K er plusset på, bliver hele leddet til 0. Ln(K) bliver til 1 over K, når vi differentierer:
Trin 3: Find MRTS ved at dividere marginalproduktet for L med marginalproduktet for K. Hvis produktionsfunktionen er en Cobb-Douglas funktion, kan du bruge en bestemt formel
Produktionsfunktionen er i dette tilfælde ikke en Cobb-Douglas funktion. Vi indsætter marginalprodukterne i den normale formel:

Trin 4: Reducer udtrykket for MRTS så meget som muligt
Her bruger vi igen regnereglen:

Læg mærke til hvordan K ”kravler” op over brøkstregerne som følge af ovenstående regel. Hver gang den kravler et trin op, skifter potensen fortegn:
MikroKogeBogen © - Marginalprodukter og MRTS - MIkroøkonomi

