Mikroøkonomi - 10.7 Pareto optimalitet - Generel ligevægt

Denne opskrift lærer dig, hvordan du løser opgaver omkring paretooptimalitet inklusiv illustration af kontraktkurven. Den fortsætter fra der hvor opskrift 10.6 slap.

I opskrift 10.6 illustrerede vi Edgeworth boksen og forbrugernes indifferenskurver. Husk at hældningerne på de to forbrugeres indifferenskurver er lig med hinanden, når kurverne tangerer.

De punkter, hvor de to forbrugeres indifferenskurver tangerer hinanden, kalder man for Pareto optimale allokeringer, og det er her, der er generel ligevægt. Pareto optimale allokeringer er således efficiente, som vi kender det ved ligevægt under fuldkommen konkurrence.

Definitionen på Pareto optimalitet er at ingen kan blive bedre stillet uden at en anden bliver dårligere stillet. Det vil sige, at de Pareto optimale allokeringer er der hvor en omfordeling af goderne vil betyde at mindst én af aktørerne vil opnå en lavere nytte.

Et andet begreb er Pareto-bedre allokeringer. Pareto-bedre betyder, at mindst én person kan stilles bedre uden at en anden stilles dårligere.

Man kan derfor også sige om de Pareto optimale allokeringer, at det er de allokeringer, hvor det ikke længere er muligt at foretage en omfordeling af varerne, som er Pareto-bedre. Derfor siger man, at der er ligevægt.

Kontraktkurven er en kurve der indeholder alle de pareto optimale allokeringer. Den del af kontraktkurven, som ligger i det linseformede areal mellem de to indifferenskurver som går igennem den initiale allokering, kaldes for ”Kernen”. På denne del af kontraktkurven ligger alle de allokeringer, som både er Pareto bedre i forhold til den initiale allokering og Pareto optimale!

Alt dette vil give bedre mening, når vi gennemgår opskriften nedenfor.

Gennemgang inkl. regneeksempel

Fortsat fra opskrift 10.6 Edgeworth box

Per og Ann ønsker begge at opnå større nytte og vil derfor forhandle med hinanden og bytte varer, hvis muligt. Ingen af dem er villige til at bytte varene på en måde, som mindsker dere nytte.

Spørgsmål a) Indtegn og forklar om der findes en eller flere allokeringer, som er Pareto-bedre i forhold til initialbeholdningen

Spørgsmål b) Indtegn en eller flere allokeringer som er Pareto optimale

Spørgsmål c) Indtegn kontraktkurven og forklar hvad denne betyder

Spørgsmål d) Hvor vil der være generel ligevægt?

Trin 1: Marker arealet mellem de to indifferenskurver, der løber igennem den initiale allokering, og forklar at alle allokeringer i dette areal er Pareto-bedre end initialbeholdningen

De to indifferenskurver, som går igennem den initiale allokering, tangerer ikke hinanden i dette punkt. Derfor er der ikke ligevægt. Det betyder at de to forbrugere vil bytte varer med hinanden for at øge deres nytte.

De Pareto-bedre allokeringer er, som nævnt, de allokeringer, hvor mindst en af forbrugerne er blevet bedre stillet, uden at den anden er blevet dårligere stillet.

Når du skal undersøge de Pareto-bedre allokeringer, skal du altid sammenligne med den initiale allokering. For at øge deres nytte skal forbrugerne kunne komme ud på en indifferenskurve, der ligger længere væk fra deres hjørne (deres 0,0 punkt, også kaldet origo) end den indifferenskurve, der løber igennem den initiale allokering.

Af nedenstående illustration kan vi se, at hvis Per og Ann forhandler sig frem til en allokering, der ligger inde i det linseformede areal mellem de to kurver, som løber igennem den initiale allokering, vil de begge have en større nytte. Inde i denne linse er de begge rykket længere væk fra deres hjørne.

Hvis de forhandler sig frem til en allokering, der ligger på ”linsens” kant, dvs. en af indifferenskurverne, så har én af dem opnået større nytte uden at den anden er blevet dårligere stillet.

Vi markerer derfor arealet mellem de to indifferenskurver, da alle punkter i dette areal inklusiv kanten på ”linsen” er Pareto-bedre end den initiale allokering. Vi har herved svaret på spørgsmål a)

Løsningen kort fortalt

Trin 1:

Marker arealet mellem de to indifferenskurver, der løber igennem initialbeholdningen, og forklar at alle allokeringer i dette areal er

Pareto-bedre end initialbeholdningen.

Trin 2:

Indtegn de Pareto optimale punkter (tangeringspunkterne mellem forbrugernes indifferenskurver) i Edgeworth boksen.

Trin 3a:

Forbind dem for at tegne kontraktkurven, og forklar at kontraktkurven løber gennem alle tangeringspunkter mellem forbrugernes indifferenskurver. Alle punkter på kontraktkurven er altså pareto optimale.

Trin 3b:

Hvis du vil tegne kontraktkurven helt præcist, kan du finde funktionen for denne: Sæt hældningen på de to forbrugeres indifferenskurver lig med hinanden, dvs. MRS1=MRS2 og isoler Y1.

Trin 4:

Marker den del af kontraktkurven, som ligger i det linseformede areal, og forklar, at alle punkter på denne del af kurven både er Pareto-bedre i forhold til den initiale allokering og Pareto optimale. Forklar at forbrugerne vil forhandle sig frem til et punkt på denne del. Den forbruger, som er den bedste forhandler, opnår størst nytte i ligevægten.

STEP-BY-STEP GUIDE TIL HVORDAN DU ILLUSTRERER SITUATIONEN FRA BUNDEN

Mikroøkonomi, Edgeworth Box, Generel ligevægt

Enhver allokering der ligger uden for linsen vil betyde, at en af forbrugerne er blevet dårligere stillet, sammenlignet med den initiale allokering, fordi punktet vil ligge på en indifferenskurve, der ligger tættere på deres hjørne og derfor vil have en lavere nytte.

Trin 2: Indtegn de Pareto optimale punkter (tangeringspunkterne mellem forbrugernes indifferenskurver) i Edgeworth boksen

De Pareto optimale punkter er, som nævnt, de punkter, hvor forbrugernes indifferenskurver tangerer hinanden. I disse punkter vil ingen af forbrugerne forhandle yderligere, da enhver omfordeling vil stille en af dem dårligere. I de Pareto optimale allokeringer er det altså ikke muligt at finde en Pareto-bedre allokering.

Rent grafisk kan vi se det ved, at hvis vi finder et punkt, der ligger på den ene eller anden side af tangeringspunktet, vil det betyde at en af forbrugerene nu er hoppet ind på en indifferenskurve, der ligger tættere på deres hjørne og derfor har lavere nytte. Se illustrationen i Trin 3a.

Trin 3a: Forbind dem for at tegne kontraktkurven, og forklar at kontraktkurven løber gennem alle tangeringspunkter mellem forbrugernes indifferenskurver. Alle punkter på kontraktkurven er altså pareto optimale

Kontraktkurven løber gennem alle tangeringspunkter mellem de to forbrugeres indifferenskurver, det vil sige alle de Pareto optimale allokeringer. Vi kan derfor blot forbinde disse punkter for at tegne kontraktkurven. Oftest behøver du ikke tegne kontraktkurven helt nøjagtigt, men hvis det er tilfældet, skal du finde en funktion for kontraktkurven og indtegne den. Det ser vi nærmere på i trin 3b

Vi har herved løst spørgsmål b) og c).

Trin 3b: Hvis du vil tegne kontraktkurven helt præcist, kan du finde funktionen for denne: Sæt hældningen på de to forbrugeres indifferenskurver lig med hinanden, dvs. MRS1=MRS2 og isoler Y1

Dette trin er oftest ikke nødvendigt, men det skal selvfølgelig afklares med underviseren, hvad der forventes til eksamen. Hvis det forventes af underviseren på dit studie, at du skal finde en funktion for kontraktkurven og indtegne denne, så læs videre, ellers kan du spring dette trin over.

I alle tangeringspunkterne mellem de to forbrugeres indifferenskurver, er hældningen på kurverne lig med hinanden. Husk at hældningen på en indifferenskurve er bytteforholdet MRS. Vi kan derfor udlede en formel for kontraktkurven ved at sætte MRS for Per lig med MRS for Ann og herefter isolere enten YPer eller YAnn, afhængigt af hvilket perspektiv vi vil tegne den fra.

Vi starter med at finde MRS for Per (hvis du er usikker på, hvordan du finder MRS, så læs opskrift 2.1 Marginalnytter og MRS). Husk at Pers nyttefunktion var givet som U=2XY (se evt. opskrift 10.6 hvor opgaven startede):

På samme måde finder vi MRS for Ann. Hendes nyttefunktion var givet ved U=XY.

Så langt så godt. Nu skal vi holde tungen lige i munden. I princippet har vi to ligninger med 4 ubekendte. Pers mængder af vare Y og X er jo ikke de samme som Y og X for Ann. Vi skelner imellem dem ved at sætte et et-tal efter Pers mængder og et to-tal efter Anns mængder:

Vi kan ikke løse to ligninger med fire ubekendte. Derfor skal vi finde nogle udtryk for Anns mængder, hvor Pers mængder indgår.

Den mængde Ann vil have af en vare svarer til den totale mængde af varen i økonomien minus Pers mængde. Vi kan skrive det således:

På samme måde for Anns mængde af vare Y:

I opskrift 10.6 beregnede vi den totale mængde af vare X til 20 og den totale mængde af vare Y til 18. Vi indsætter dette i ovenstående formler for Anns mængder af varene:

Vi kan nu sætte MRS for Per og Ann lig med hinanden og sætte ovenstående formler ind i stedet for Anns mængder:

Nu isolerer vi Pers mængde af Y, dvs. Y1:

Vi har forsøgt at have så mange mellemregninger med som muligt, da det kan være svært at overskue matematikken i sådan en ligningsløsning. Se evt. opskrift 0.3 Matematiske regneregler hvis nødvendigt.

Vi har nu fundet frem til ligningen for kontraktkurven og kan således blot udfylde et sildeben for at finde punkterne på kurven:

Nu da vi har punkterne, som jo er de Pareto optimale punkter, kan vi indtegne dem og forbinde dem for at illustrere kontraktkurven.

Bemærk at de indifferenskurver vi tegnede ind i opskrift 10.6, som nævnt vil være en anelse upræcise, hvilket vi nu kan se, da tangeringspunkterne ligger lidt uden for kontraktkurven. Dette er næsten uundgåeligt, så længe vi skal indtegne indifferenskurver, som er konvekse (buede). Hvis de skulle tegnes helt præcist, skulle vi have samtlige punkter på kurven, hvilket aldrig vil forventes. Kontraktkurven er derimod linæer i dette tilfælde og derfor præcis:

Trin 4: Marker den del af kontraktkurven, som ligger i det linseformede areal, og forklar, at alle punkter på denne del af kurven både er Pareto-bedre i forhold til den initiale allokering og Pareto optimale. Forklar at forbrugerne vil forhandle sig frem til et punkt på denne del. Den forbruger, som er den bedste forhandler, opnår størst nytte i ligevægten

Lad os starte med at identificere den del af kontraktkurven, som ligger inde i ”linsen”. Denne del af kontraktkurven kaldes ”Kernen” og indeholder, som nævnt i introduktionen, alle de allokeringer, som både er Pareto optimale og Pareto-bedre i forhold til den initiale allokering

Som nævnt i trin 1, er alle allokeringer inde i arealet af ”linsen”, inklusiv kanterne, Pareto-bedre sammenlignet med den initiale allokering. Samtidig ved vi fra trin 3, at alle punkter på kontraktkurven er Pareto optimale og derved efficiente.

Forbrugerne vil således bytte varer med hinanden, indtil der er ligevægt i økonomien. Da ingen vil acceptere et tab i nytte, skal den nye allokering som minimum være Pareto-bedre, dvs. ligge inde i linsen (eller på kanten). Samtidig vil de fortsætte med at forhandle, indtil der er ligevægt, dvs. indtil de når en Pareto optimal allokering. Heraf må vi konkludere, at de vil forhandle sig frem til en ny allokering af varene, som ligger på ”Kernen”. Hvilken specifik allokering de ender med afhænger af forbrugernes forhandlingsevner. Hvis Per f.eks. var meget dårligere til at forhandle end Ann, kunne ligevægten ende med ligge på kanten af ”linsen”, i det punkt der er tættest på Pers hjørne. Per vil således opnå samme nytte, som i den initiale allokering (da han vil ligge på samme indifferenskurve), mens Ann vil øge sin nytte betydeligt.

Der vil være generel ligevægt i en af de allokeringer, som ligger på ”Kernen”, og vi har herved svaret på spørgsmål d). På nedenstående illustration er markeret et muligt ligevægtspunkt på ”Kernen”:

STEP BY STEP GUIDE TIL ILLUSTRATION:

I nedenstående slideshow har vi samlet illustrationerne fra denne opskrift samt opskrift 10.6 Edgeworth Box i en "step by step" guide. Den viser, hvordan du illustrerer hele processen for generel ligevægt fra start til slut.

Step 1 Klik på højrepilen for næste step eller på billedet for at forstørre	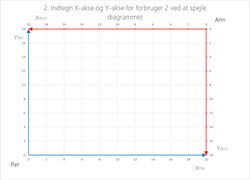Step 2 Klik på højrepilen for næste step eller på billedet for at forstørre	Step 3 Klik på højrepilen for næste step eller på billedet for at forstørre
Step 4 Klik på højrepilen for næste step eller på billedet for at forstørre	Step 5 Klik på højrepilen for næste step eller på billedet for at forstørre	Step 6 Klik på højrepilen for næste step eller på billedet for at forstørre
Step 7 Klik på højrepilen for næste step eller på billedet for at forstørre	Step 8 Klik på højrepilen for næste step eller på billedet for at forstørre	Step 9 Klik på billedet for at forstørre